Can a Team Consistently Beat the Spread?
Loud noise is still noise
A fun question was posed recently by @matsonj on Twitter asking whether a sports team can consistently beat the spread. The short answer is no, and here's why:
(Btw if you want to throw questions my way on Twitter go for it @DaniMermelstein)
So first off, the “spread” represents the mid-range expected score difference for a game: eg Suns have a 50% chance to win by 6 points. Then everybody bets on the over/under. If a sportsbook does their job correctly then over many games a team will cover the spread 50% of the time. Here is what the cover rate looks like for the 2021-22 regular season:
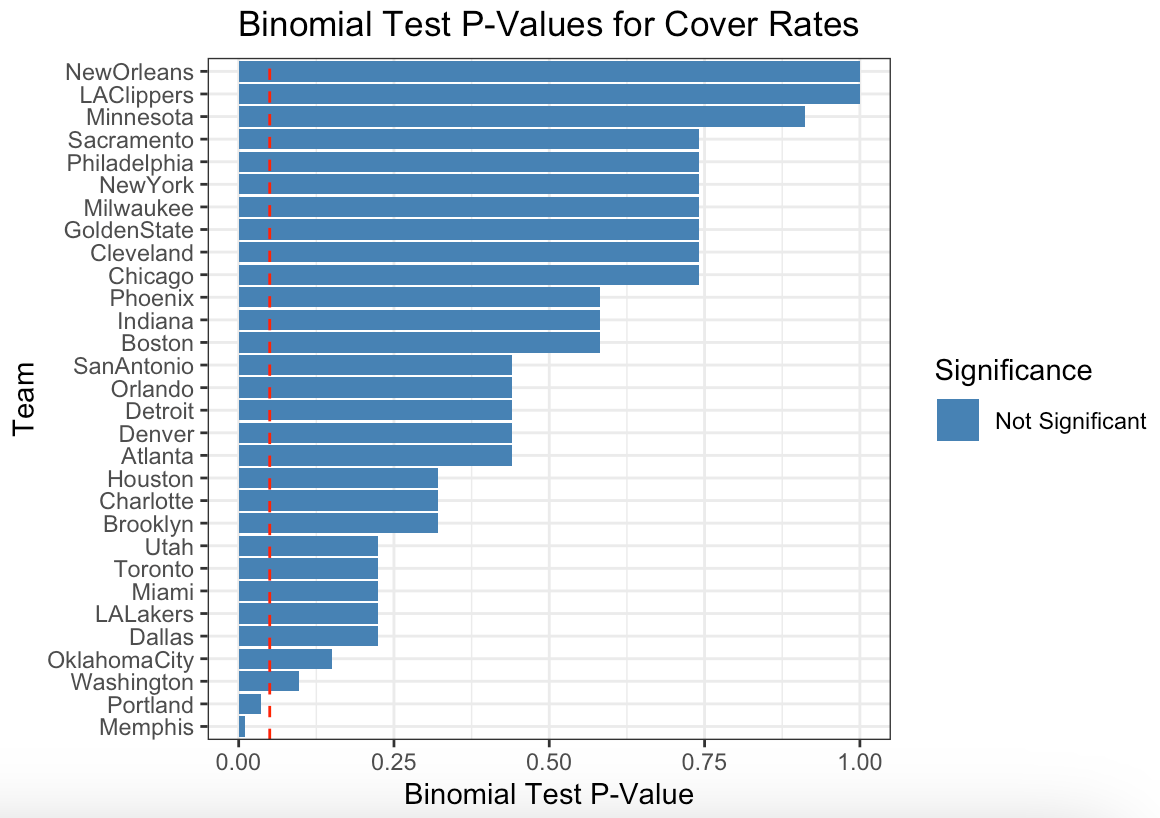
When we look at these rates, we can ask: does any team cover the spread (or not) at an unexpected rate? Portland, Washington and Memphis look interesting 🤷. We can then run a binomial test to check whether any of these rates deviate from 50%.
Portland and Memphis' cover rate has a p-value smaller than 0.05. But we have 30 teams in the dataset, so we should expect 1-to-2 p-values in that set to randomly fall under that threshold (false positives). So what now?
More math coming right at you: To correct for the false discovery rate we can use the Benjamini-Hochberg method. And once we run the numbers through that we find… that none of those p-values are significant.
So what do we take away from this?
Teams can have streaks throughout the season, but we should expect the rate at which a team covers the spread to converge on 50% over time. Don't fall for claims that a team consistently covers the spread.